Social Media Lab

In [1]:

import pandas as pd

# Load the CSV file
memespector_file = "/content/drive/MyDrive/2024-01-09-Bauernproteste/2024-01-11-Google-Vision-All.csv"
df = pd.read_csv(memespector_file)

df = df[['Image_BaseName', 'GV_Label_Descriptions']]

# Splitting the 'GV_Label_Descriptions' into individual labels
split_labels = df['GV_Label_Descriptions'].str.split(';').apply(pd.Series, 1).stack()
split_labels.index = split_labels.index.droplevel(-1)  # to line up with df's index
split_labels.name = 'Label'

# Joining the split labels with the original dataframe
df_split = df.join(split_labels)

# Creating a matrix of True/False values for each label per Image_BaseName
matrix = pd.pivot_table(df_split, index='Image_BaseName', columns='Label', aggfunc=lambda x: True, fill_value=False)

# Resetting the column headers to be the label names only
matrix.columns = [col[1] for col in matrix.columns.values]

# Now 'matrix' has a single level of column headers with only the label names

In [2]:

matrix

	Adaptation	Advertising	Afterglow	Agricultural machinery	Agriculture	Air travel	Aircraft	Airliner	Airplane	Alloy wheel	...	Vertebrate	Water	Water resources	Wheel	Whiskers	White	Window	Wood	Working animal	World
Image_BaseName
6750551853789891846.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
6750761577349254405.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
6751467034741067014.jpg	False	False	False	False	True	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
6763591353164254469.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
6766552734108749062.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
7321800737606896928.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
7321804342179204384.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
7321804909290999045.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	True	False	False	False	False	False	False
7321806774967815457.jpg	True	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
7321806890906701089.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False

982 rows × 681 columns

In [3]:

from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np

# Ensuring that 'Image_BaseName' is not part of the matrix to apply PCA
image_base_names = matrix.index  # Saving the image base names for later use
label_matrix = matrix.values  # Convert to numpy array for PCA

# Dimensionality reduction using PCA
# Considering a variance ratio of 0.95 to determine the number of components
pca = PCA(n_components=0.95)
matrix_reduced = pca.fit_transform(label_matrix)

# If needed, you can create a DataFrame from the PCA-reduced matrix and reattach the 'Image_BaseName' column
matrix_reduced_df = pd.DataFrame(matrix_reduced, index=image_base_names)

In [4]:

matrix_reduced_df

	0	1	2	3	4	5	6	7	8	9	...	232	233	234	235	236	237	238	239	240	241
Image_BaseName
6750551853789891846.jpg	1.392793	-0.851573	-0.225060	-0.630954	0.345822	-0.313126	0.376667	0.370456	-0.012519	-0.898472	...	-0.007803	0.022912	-0.002782	0.019272	-0.005465	-0.005129	0.011833	0.000200	0.006499	0.010995
6750761577349254405.jpg	-1.045212	0.139963	-0.396712	0.505531	-0.186165	0.278001	0.860551	-0.387782	-0.041959	0.146992	...	0.020865	0.027422	0.064993	0.046791	0.042511	-0.040843	-0.091713	-0.064683	0.043392	-0.045372
6751467034741067014.jpg	0.364738	0.089808	0.603463	0.717136	0.084382	0.130516	0.835040	0.056190	-0.175465	-0.551632	...	-0.009497	0.144801	-0.020713	0.035502	-0.085562	-0.169911	0.083582	0.045916	-0.123521	0.032273
6763591353164254469.jpg	0.657532	-0.007257	-0.226448	-0.142833	-0.615043	-0.208217	-0.082478	0.181550	0.899774	0.462160	...	-0.025889	0.006257	0.060421	0.028564	0.045773	0.000179	0.003499	0.027838	0.007171	-0.051516
6766552734108749062.jpg	1.638604	-0.418596	-0.178993	-0.522654	0.663303	-0.186928	1.000894	-0.307874	-0.172688	0.336597	...	-0.009052	-0.002043	0.007575	-0.031553	0.007831	-0.005779	-0.023599	-0.021165	-0.000496	-0.006467
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
7321800737606896928.jpg	-0.698156	0.191274	-0.529836	0.047008	0.862388	-0.111187	-0.390502	-0.089231	0.144091	0.326504	...	-0.015025	-0.068188	-0.023787	0.009343	0.004624	0.001396	0.097441	0.145987	-0.102992	0.110626
7321804342179204384.jpg	0.032051	0.048450	0.454149	-0.012114	0.395014	0.128612	0.042362	1.019634	-0.367217	1.025644	...	-0.002146	-0.042328	0.114229	-0.066740	-0.051395	-0.021397	0.012134	0.046365	-0.005712	0.036329
7321804909290999045.jpg	1.005015	0.923683	0.371054	0.533427	0.356759	0.813597	0.087288	-0.289707	0.377865	1.242866	...	0.005721	0.000672	0.021087	0.020260	0.037709	0.000290	0.015725	0.013237	0.018040	-0.002060
7321806774967815457.jpg	-0.597974	0.855850	-0.262498	-0.214283	-0.731812	-0.209626	-0.179683	0.529353	-0.239506	0.048401	...	-0.012399	0.023383	-0.073488	0.063523	0.013320	0.020351	-0.033865	0.029809	-0.080413	-0.074329
7321806890906701089.jpg	-0.042383	-0.138050	0.075564	-0.396196	0.056236	0.612394	-0.272538	-0.230238	-0.379339	-0.668773	...	-0.106623	-0.214393	0.209117	0.021869	0.220278	0.070092	-0.198979	0.140981	-0.004653	-0.070667

982 rows × 242 columns

In [5]:

# Elbow method to determine optimal number of clusters
inertia = []
range_values = range(1, 20)  # Checking for 1 to 10 clusters

for i in range_values:
    kmeans = KMeans(n_clusters=i, n_init=10, random_state=0)
    kmeans.fit(matrix_reduced_df)
    inertia.append(kmeans.inertia_)

# Plotting the Elbow Curve
plt.figure(figsize=(10, 6))
plt.plot(range_values, inertia, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()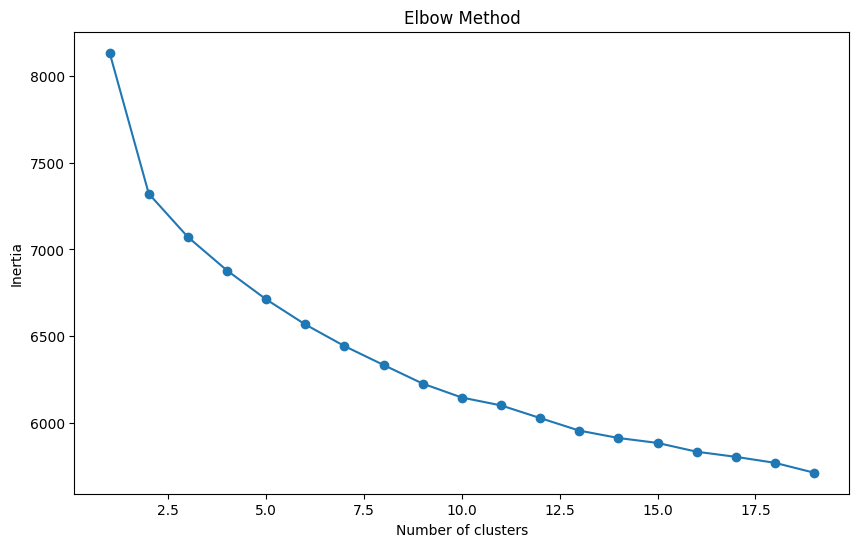

In [11]:

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt

# Define the range of clusters to try
range_values = range(2, 20)

silhouette_scores = []

# Perform k-means clustering and compute silhouette scores
for i in range_values:
    try:
        kmeans = KMeans(n_clusters=i, n_init=10, random_state=0)
        kmeans.fit(matrix_reduced_df)
        score = silhouette_score(matrix_reduced_df, kmeans.labels_)
        silhouette_scores.append(score)
    except Exception as e:
        print(f"An error occurred with {i} clusters: {e}")

# Plotting the Silhouette Scores
with plt.style.context('seaborn-whitegrid'):
    plt.figure(figsize=(10, 6))
    plt.plot(range_values, silhouette_scores, marker='o')
    plt.title('Silhouette Method')
    plt.xlabel('Number of clusters')
    plt.ylabel('Silhouette Score')
    plt.show()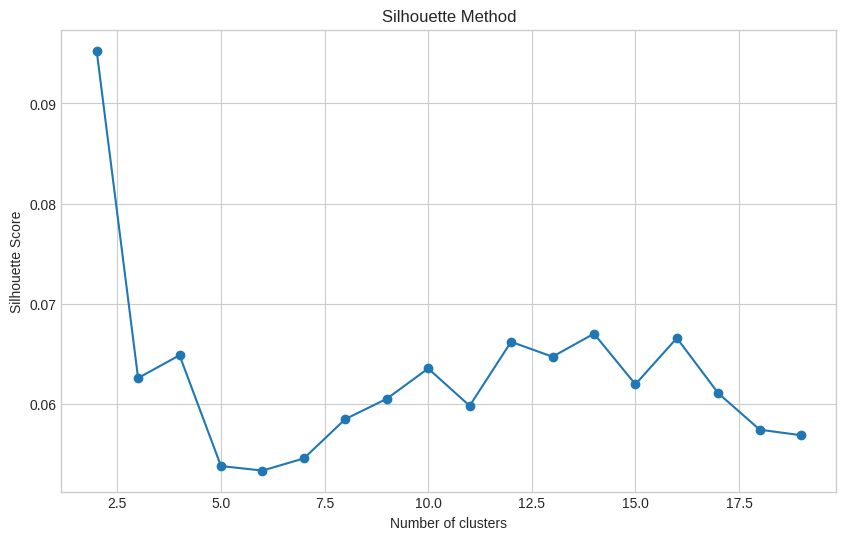

In [8]:

# Final k-means clustering using n clusters
kmeans_final = KMeans(n_clusters=11, n_init=10, random_state=0)
clusters = kmeans_final.fit_predict(matrix_reduced)

# Adding the cluster information back to the original dataframe
matrix['Cluster'] = clusters

In [12]:

# Displaying the first few rows of the dataframe with cluster information
matrix.head()

	Adaptation	Advertising	Afterglow	Agricultural machinery	Agriculture	Air travel	Aircraft	Airliner	Airplane	Alloy wheel	...	Water	Water resources	Wheel	Whiskers	White	Window	Wood	Working animal	World	Cluster
Image_BaseName
6750551853789891846.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	8
6750761577349254405.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	2
6751467034741067014.jpg	False	False	False	False	True	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	6
6763591353164254469.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	0
6766552734108749062.jpg	False	False	False	False	False	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	8

5 rows × 682 columns

In [2]:

!unzip /content/drive/MyDrive/2024-01-09-Bauernproteste/2024-01-09-Images-Clean.zip

In [3]:

# Display the result. See linked notebook for code.